当前位置：首页 > PHP教程 > php高级应用 > 列表

布隆过滤器(bloom filter)及php和redis实现布隆过滤器的方法

发布:smiling　来源: PHP粉丝网 　添加日期：2022-01-26 09:29:14　浏览: 评论：0　

这篇文章主要介绍了布隆过滤器(bloom filter)介绍以及php和redis实现布隆过滤器实现方法,非常不错，具有一定的参考借鉴价值，需要的朋友可以参考下。

引言

在介绍布隆过滤器之前我们首先引入几个场景。

场景一

在一个高并发的计数系统中，如果一个key没有计数，此时我们应该返回0，但是访问的key不存在，相当于每次访问缓存都不起作用了，那么如何避免频繁访问数量为0的key而导致的缓存被击穿？

有人说， 将这个key的值置为0存入缓存不就行了吗？确实，这是一个好的方案。大部分情况我们都是这样做的，当访问一个不存在的key的时候，设置一个带有过期时间的标志，然后放入缓存。不过这样做的缺点也很明显，浪费内存和无法抵御随机key攻击。

场景二

在一个黑名单系统中，我们需要设置很多黑名单内容。比如一个邮件系统，我们需要设置黑名单用户，当判断垃圾邮件的时候，要怎么去做。比如爬虫系统，我们要记录下来已经访问过的链接避免下次访问重复的链接。

在邮件很少或者用户很少的情况下，我们用普通数据库自带的查询就能完成。在数据量太多的时候，为了保证速度，通常情况下我们会将结果缓存到内存中，数据结构用hash表。这种查找的速度是O(1)，但是内存消耗也是惊人的。打个比方，假如我们要存10亿条数据，每条数据平均占据32个字节，那么需要的内存是64G，这已经是一个惊人的大小了。

一种解决思路

能不能有一种思路，查询的速度是O(1)，消耗内存特别小呢？前辈门早就想出了一个很好的解决方案。由于上面说的场景判断的结果只有两种状态（是或者不是，存在或者不存在），那么对于所存的数据完全可以用位来表示！数据本身则可以通过一个hash函数计算出一个key，这个key是一个位置，而这个key所对的值就是0或者1（因为只有两种状态），如下图：

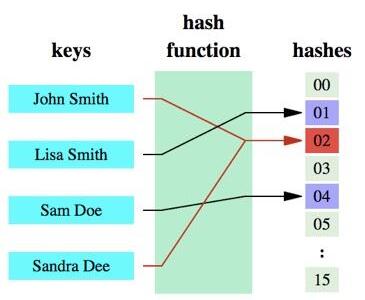
bloom redis php过滤器

布隆过滤器原理

上面的思路其实就是布隆过滤器的思想，只不过因为hash函数的限制，多个字符串很可能会hash成一个值，为了解决这个问题，布隆过滤器引入多个hash函数来降低误判率。

下图表示有三个hash函数，比如一个集合中有x，y，z三个元素，分别用三个hash函数映射到二进制序列的某些位上，假设我们判断w是否在集合中，同样用三个hash函数来映射，结果发现取得的结果不全为1，则表示w不在集合里面。

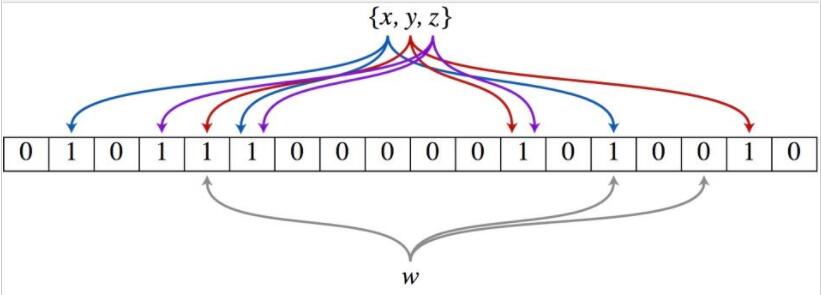
bloom redis php过滤器

布隆过滤器处理流程

布隆过滤器应用很广泛，比如垃圾邮件过滤，爬虫的url过滤，防止缓存击穿等等。下面就来说说布隆过滤器的一个完整流程，相信读者看到这里应该能明白布隆过滤器是怎样工作的。

第一步：开辟空间

开辟一个长度为m的位数组（或者称二进制向量），这个不同的语言有不同的实现方式，甚至你可以用文件来实现。

第二步：寻找hash函数

获取几个hash函数，前辈们已经发明了很多运行良好的hash函数，比如BKDRHash，JSHash，RSHash等等。这些hash函数我们直接获取就可以了。

第三步：写入数据

将所需要判断的内容经过这些hash函数计算，得到几个值，比如用3个hash函数，得到值分别是1000，2000，3000。之后设置m位数组的第1000，2000，3000位的值位二进制1。

第四步：判断

接下来就可以判断一个新的内容是不是在我们的集合中。判断的流程和写入的流程是一致的。

误判问题

布隆过滤器虽然很高效（写入和判断都是O(1)，所需要的存储空间极小），但是缺点也非常明显，那就是会误判。当集合中的元素越来越多，二进制序列中的1的个数越来越多的时候，判断一个字符串是否在集合中就很容易误判，原本不在集合里面的字符串会被判断在集合里面。

数学推导

布隆过滤器原理十分简单，但是hash函数个数怎么去判断，误判率有多少？

假设二进制序列有m位，那么经过当一个字符串hash到某一位的概率为：

1m

也就是说当前位被反转为1的概率：

p(1)=1m

那么这一位没有被反转的概率为：

p(0)=1−1m

假设我们存入n各元素，使用k个hash函数，此时没有被翻转的概率为：

p(0)=(1−1m)nk

那什么情况下我们会误判呢，就是原本不应该被翻转的位，结果翻转了，也就是

p(误判)=1−(1−1m)nk

由于只有k个hash函数同时误判了，整体才会被误判，最后误判的概率为

p(误判)=(1−(1−1m)nk)k

要使得误判率最低，那么我们需要求误判与m、n、k之间的关系，现在假设m和n固定，我们计算一下k。可以首先看看这个式子：

(1−1m)nk

由于我们的m很大，通常情况下我们会用2^32来作为m的值。上面的式子中含有一个重要极限

limx→∞(1+1x)x=e

因此误判率的式子可以写成

p(误判)=(1−(e)−nk/m)k

接下来令t=−n/m，两边同时取对数，求导，得到：

p′1p=ln(1−etk)+klnet(−etk)1−etk

让p′=0，则等式后面的为0，最后整理出来的结果是

(1−etk)ln(1−etk)=etklnetk

计算出来的k为ln2mn，约等于0.693mn，将k代入p(误判)，我们可以得到概率和m、n之间的关系，最后的结果

(1/2)ln2mn，约等于0.6185m/n

以上我们就得出了最佳hash函数个数以及误判率与mn之前的关系了。

下表是m与n比值在k个hash函数下面的误判率

  1. m/n k k=1 k=2 k=3 k=4 k=5 k=6 k=7 k=8 
  2. 2 1.39 0.393 0.400       
  3. 3 2.08 0.283 0.237 0.253      
  4. 4 2.77 0.221 0.155 0.147 0.160     
  5. 5 3.46 0.181 0.109 0.092 0.092 0.101    
  6. 6 4.16 0.154 0.0804 0.0609 0.0561 0.0578 0.0638   
  7. 7 4.85 0.133 0.0618 0.0423 0.0359 0.0347 0.0364   
  8. 8 5.55 0.118 0.0489 0.0306 0.024 0.0217 0.0216 0.0229  
  9. 9 6.24 0.105 0.0397 0.0228 0.0166 0.0141 0.0133 0.0135 0.0145 
  10. 10 6.93 0.0952 0.0329 0.0174 0.0118 0.00943 0.00844 0.00819 0.00846 
  11. 11 7.62 0.0869 0.0276 0.0136 0.00864 0.0065 0.00552 0.00513 0.00509 
  12. 12 8.32 0.08 0.0236 0.0108 0.00646 0.00459 0.00371 0.00329 0.00314 
  13. 13 9.01 0.074 0.0203 0.00875 0.00492 0.00332 0.00255 0.00217 0.00199 
  14. 14 9.7 0.0689 0.0177 0.00718 0.00381 0.00244 0.00179 0.00146 0.00129 
  15. 15 10.4 0.0645 0.0156 0.00596 0.003 0.00183 0.00128 0.001 0.000852 
  16. 16 11.1 0.0606 0.0138 0.005 0.00239 0.00139 0.000935 0.000702 0.000574 
  17. 17 11.8 0.0571 0.0123 0.00423 0.00193 0.00107 0.000692 0.000499 0.000394 
  18. 18 12.5 0.054 0.0111 0.00362 0.00158 0.000839 0.000519 0.00036 0.000275 
  19. 19 13.2 0.0513 0.00998 0.00312 0.0013 0.000663 0.000394 0.000264 0.000194 
  20. 20 13.9 0.0488 0.00906 0.0027 0.00108 0.00053 0.000303 0.000196 0.00014 
  21. 21 14.6 0.0465 0.00825 0.00236 0.000905 0.000427 0.000236 0.000147 0.000101 
  22. 22 15.2 0.0444 0.00755 0.00207 0.000764 0.000347 0.000185 0.000112 7.46e-05 
  23. 23 15.9 0.0425 0.00694 0.00183 0.000649 0.000285 0.000147 8.56e-05 5.55e-05 
  24. 24 16.6 0.0408 0.00639 0.00162 0.000555 0.000235 0.000117 6.63e-05 4.17e-05 
  25. 25 17.3 0.0392 0.00591 0.00145 0.000478 0.000196 9.44e-05 5.18e-05 3.16e-05 
  26. 26 18 0.0377 0.00548 0.00129 0.000413 0.000164 7.66e-05 4.08e-05 2.42e-05 
  27. 27 18.7 0.0364 0.0051 0.00116 0.000359 0.000138 6.26e-05 3.24e-05 1.87e-05 
  28. 28 19.4 0.0351 0.00475 0.00105 0.000314 0.000117 5.15e-05 2.59e-05 1.46e-05 
  29. 29 20.1 0.0339 0.00444 0.000949 0.000276 9.96e-05 4.26e-05 2.09e-05 1.14e-05 
  30. 30 20.8 0.0328 0.00416 0.000862 0.000243 8.53e-05 3.55e-05 1.69e-05 9.01e-06 
  31. 31 21.5 0.0317 0.0039 0.000785 0.000215 7.33e-05 2.97e-05 1.38e-05 7.16e-06 
  32. 32 22.2 0.0308 0.00367 0.000717 0.000191 6.33e-05 2.5e-05 1.13e-05 5.73e-06 

php+Redis实现的布隆过滤器

由于Redis实现了setbit和getbit操作，天然适合实现布隆过滤器，redis也有布隆过滤器插件。这里使用php+redis实现布隆过滤器。

首先定义一个hash函数集合类，这些hash函数不一定都用到，实际上32位hash值的用3个就可以了，具体的数量可以根据你的位序列总量和你需要存入的量决定，上面已经给出最佳值。

  1. class BloomFilterHash 
  2. { 
  3.  /** 
  4.  * 由Justin Sobel编写的按位散列函数 
  5.  */ 
  6.  public function JSHash($string, $len = null) 
  7.  { 
  8.   $hash = 1315423911; 
  9.   $len || $len = strlen($string); 
  10.   for ($i=0; $i<$len; $i++) { 
  11.   $hash ^= (($hash << 5) + ord($string[$i]) + ($hash >> 2)); 
  12.   } 
  13.  return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF; 
  14.  } 
  15.  
  16.  /** 
  17.  * 该哈希算法基于AT＆T贝尔实验室的Peter J. Weinberger的工作。 
  18.  * Aho Sethi和Ulman编写的“编译器（原理，技术和工具）”一书建议使用采用此特定算法中的散列方法的散列函数。 
  19.  */ 
  20.  public function PJWHash($string, $len = null) 
  21.  { 
  22.  $bitsInUnsignedInt = 4 * 8; //（unsigned int）（sizeof（unsigned int）* 8）; 
  23.   $threeQuarters = ($bitsInUnsignedInt * 3) / 4; 
  24.   $oneEighth = $bitsInUnsignedInt / 8; 
  25.   $highBits = 0xFFFFFFFF << (int) ($bitsInUnsignedInt - $oneEighth); 
  26.   $hash = 0; 
  27.   $test = 0; 
  28.   $len || $len = strlen($string); 
  29.   for($i=0; $i<$len; $i++) { 
  30.  $hash = ($hash << (int) ($oneEighth)) + ord($string[$i]); } $test = $hash & $highBits; if ($test != 0) { $hash = (($hash ^ ($test >> (int)($threeQuarters))) & (~$highBits)); 
  31.   } 
  32.  return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF; 
  33.  } 
  34.  
  35.  /** 
  36.  * 类似于PJW Hash功能，但针对32位处理器进行了调整。它是基于UNIX的系统上的widley使用哈希函数。 
  37.  */ 
  38.  public function ELFHash($string, $len = null) 
  39.  { 
  40.  $hash = 0; 
  41.  $len || $len = strlen($string); 
  42.   for ($i=0; $i<$len; $i++) { 
  43.    $hash = ($hash << 4) + ord($string[$i]); $x = $hash & 0xF0000000; if ($x != 0) { $hash ^= ($x >> 24); 
  44.    } 
  45.    $hash &= ~$x; 
  46.   } 
  47.  return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF; 
  48.  } 
  49.  
  50.  /** 
  51.  * 这个哈希函数来自Brian Kernighan和Dennis Ritchie的书“The C Programming Language”。 
  52.  * 它是一个简单的哈希函数，使用一组奇怪的可能种子，它们都构成了31 .... 31 ... 31等模式，它似乎与DJB哈希函数非常相似。 
  53.  */ 
  54.  public function BKDRHash($string, $len = null) 
  55.  { 
  56.   $seed = 131; # 31 131 1313 13131 131313 etc.. 
  57.   $hash = 0; 
  58.   $len || $len = strlen($string); 
  59.   for ($i=0; $i<$len; $i++) { 
  60.    $hash = (int) (($hash * $seed) + ord($string[$i])); 
  61.   } 
  62.  return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF; 
  63.  } 
  64.  
  65.  /** 
  66.  * 这是在开源SDBM项目中使用的首选算法。 
  67.  * 哈希函数似乎对许多不同的数据集具有良好的总体分布。它似乎适用于数据集中元素的MSB存在高差异的情况。 
  68.  */ 
  69.  public function SDBMHash($string, $len = null) 
  70.  { 
  71.  $hash = 0; 
  72.  $len || $len = strlen($string); 
  73.  for ($i=0; $i<$len; $i++) { 
  74.  $hash = (int) (ord($string[$i]) + ($hash << 6) + ($hash << 16) - $hash); 
  75.  } 
  76.  return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF; 
  77.  } 
  78.  
  79.  /** 
  80.  * 由Daniel J. Bernstein教授制作的算法，首先在usenet新闻组comp.lang.c上向世界展示。 
  81.  * 它是有史以来发布的最有效的哈希函数之一。 
  82.  */ 
  83.  public function DJBHash($string, $len = null) 
  84.  { 
  85.  $hash = 5381; 
  86.  $len || $len = strlen($string); 
  87.  for ($i=0; $i<$len; $i++) { 
  88.  $hash = (int) (($hash << 5) + $hash) + ord($string[$i]); 
  89.  } 
  90.  return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF; 
  91.  } 
  92.  
  93.  /** 
  94.  * Donald E. Knuth在“计算机编程艺术第3卷”中提出的算法，主题是排序和搜索第6.4章。 
  95.  */ 
  96.  public function DEKHash($string, $len = null) 
  97.  { 
  98.  $len || $len = strlen($string); 
  99.  $hash = $len; 
  100.  for ($i=0; $i<$len; $i++) { 
  101.  $hash = (($hash << 5) ^ ($hash >> 27)) ^ ord($string[$i]); 
  102.  } 
  103.  return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF; 
  104.  } 
  105.  
  106.  /** 
  107.  * 参考 http://www.isthe.com/chongo/tech/comp/fnv/ 
  108.  */ 
  109.  public function FNVHash($string, $len = null) 
  110.  { 
  111.  $prime = 16777619; //32位的prime 2^24 + 2^8 + 0x93 = 16777619 
  112.  $hash = 2166136261; //32位的offset 
  113.  $len || $len = strlen($string); 
  114.  for ($i=0; $i<$len; $i++) { 
  115.  $hash = (int) ($hash * $prime) % 0xFFFFFFFF; 
  116.  $hash ^= ord($string[$i]); 
  117.  } 
  118.  return ($hash % 0xFFFFFFFF) & 0xFFFFFFFF; 
  119.  } 
  120. } 

接着就是连接redis来进行操作

  1. /** 
  2.  * 使用redis实现的布隆过滤器 
  3.  */ 
  4. abstract class BloomFilterRedis 
  5. { 
  6.  /** 
  7.  * 需要使用一个方法来定义bucket的名字 
  8.  */ 
  9.  protected $bucket; 
  10.  
  11.  protected $hashFunction; 
  12.  
  13.  public function __construct($config, $id) 
  14.  { 
  15.  if (!$this->bucket || !$this->hashFunction) { 
  16.  throw new Exception("需要定义bucket和hashFunction", 1); 
  17.  } 
  18.  $this->Hash = new BloomFilterHash; 
  19.  $this->Redis = new YourRedis; //假设这里你已经连接好了 
  20.  } 
  21.  
  22.  /** 
  23.  * 添加到集合中 
  24.  */ 
  25.  public function add($string) 
  26.  { 
  27.  $pipe = $this->Redis->multi(); 
  28.  foreach ($this->hashFunction as $function) { 
  29.  $hash = $this->Hash->$function($string); 
  30.  $pipe->setBit($this->bucket, $hash, 1); 
  31.  } 
  32.  return $pipe->exec(); 
  33.  } 
  34.  
  35.  /** 
  36.  * 查询是否存在, 存在的一定会存在, 不存在有一定几率会误判 
  37.  */ 
  38.  public function exists($string) 
  39.  { 
  40.  $pipe = $this->Redis->multi(); 
  41.  $len = strlen($string); 
  42.  foreach ($this->hashFunction as $function) { 
  43.  $hash = $this->Hash->$function($string, $len); 
  44.  $pipe = $pipe->getBit($this->bucket, $hash); 
  45.  } 
  46.  $res = $pipe->exec(); 
  47.  foreach ($res as $bit) { 
  48.  if ($bit == 0) { 
  49.  return false; 
  50.  } 
  51.  } 
  52.  return true; 
  53.  } 
  54.  
  55. } 

上面定义的是一个抽象类，如果要使用，可以根据具体的业务来使用，比如下面是一个过滤重复内容的过滤器。

  1. /** 
  2.  * 重复内容过滤器 
  3.  * 该布隆过滤器总位数为2^32位, 判断条数为2^30条. hash函数最优为3个.(能够容忍最多的hash函数个数) 
  4.  * 使用的三个hash函数为 
  5.  * BKDR, SDBM, JSHash 
  6.  * 
  7.  * 注意, 在存储的数据量到2^30条时候, 误判率会急剧增加, 因此需要定时判断过滤器中的位为1的的数量是否超过50%, 超过则需要清空. 
  8.  */ 
  9. class FilteRepeatedComments extends BloomFilterRedis 
  10. { 
  11.  /** 
  12.  * 表示判断重复内容的过滤器 
  13.  * @var string 
  14.  */ 
  15.  protected $bucket = 'rptc'; 
  16.  
  17.  protected $hashFunction = array('BKDRHash', 'SDBMHash', 'JSHash'); 
  18. }

Tags: bloom redis php过滤器

分享到：

相关文章

推荐文章

热门文章

最新评论文章